
|
Note: This tutorial is being developed! For a comprehensive
tutorial on quantum computing, visit
Qiskit Tutorial.
|
Operations on standard computers are based on electronic devices processing digital information, i.e. input and output signals for each device are either low or high and correspond to logical ‘0’ or ‘1’. All data is represented by a series for 0’s and 1’s, e.g. the number 5 (decimal) is represented by 101 (binary): 5 = 4 + 1 = 1×22+0×21+1×20. Digits in this binary base are called bits. Each bit carries exactly one value: either 0 or 1. All operations on bits are deterministic: results of any operation can be predicted with certainty.
Quantum objects, on the other hand, exist in all possible states simultaneously, although with different probabilities. We may assign a state vector |ψ> to the object, which contains the (complex) amplitudes Ak for each state. The probability for finding the object in any state is given by P(k)=|Ak|2, and since the probability is 100\% for finding the quantum object in any state, the sum over all P(k) must be equal to 1. A measurement performed on a quantum object yields the probability of finding the object in the measured state.
A simple quantum object is the spin of an electron, which can hold only 2 values when measured: +ℏ/2 or -ℏ/2 (its states are denoted as |↑> and |↓> or as |0> and |1> kets); in other words: the spin, i.e. the intrinsic magnet moment, of an electron cannot take arbitrary values but is quantized. Such measurements can be performed by sending an electron (or ion) beam through an inhomogeneous magnetic field (Stern-Gerlach Experiment; animation of the experiment). The beam is split into an upward (positive) and downward (negative) beam. A measurement of the spin can be regarded as measuring the projection of the electron spin onto the possible states that the system can take. Since there are only 2 states in this system, a measurement yields either upward or downward deflection, for each electron by the same amount. The probability of up- or downward deflection depends on the initial orientation of the spin; if it were initially exactly horizontal, there would be a 50-50 chance to measure it in the top or in the botton beam.
In contrast, a classical beam of tiny magnets would be deflected by the magnetic field over a range in the vertical direction, depending on the initial orientation of the magnets; maximum deflection occurs for vertically oriented magnets, no reflection for horizontally oriented magnets, and various amounts of deflection for partially vertical orientation. In other words, the amount of deflection depends on the projection of the magnet onto the vertical direction.
The z-component of the spin is measured if the magnetic field is oriented in z-direction as shown in the figure on the left. The figure on the right shows the corresponding magnet orientation for measuring along the x-direction.
 |

|

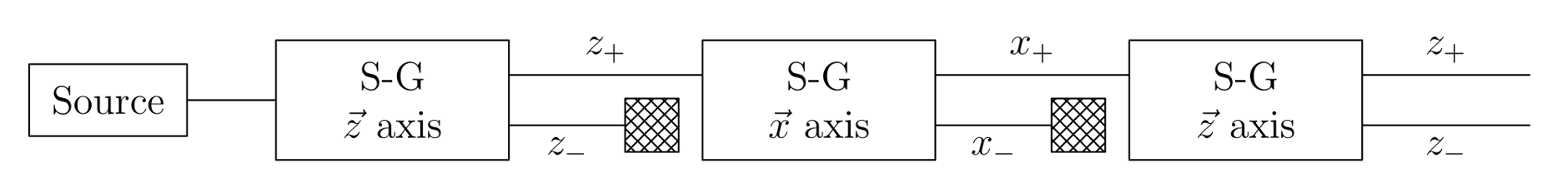
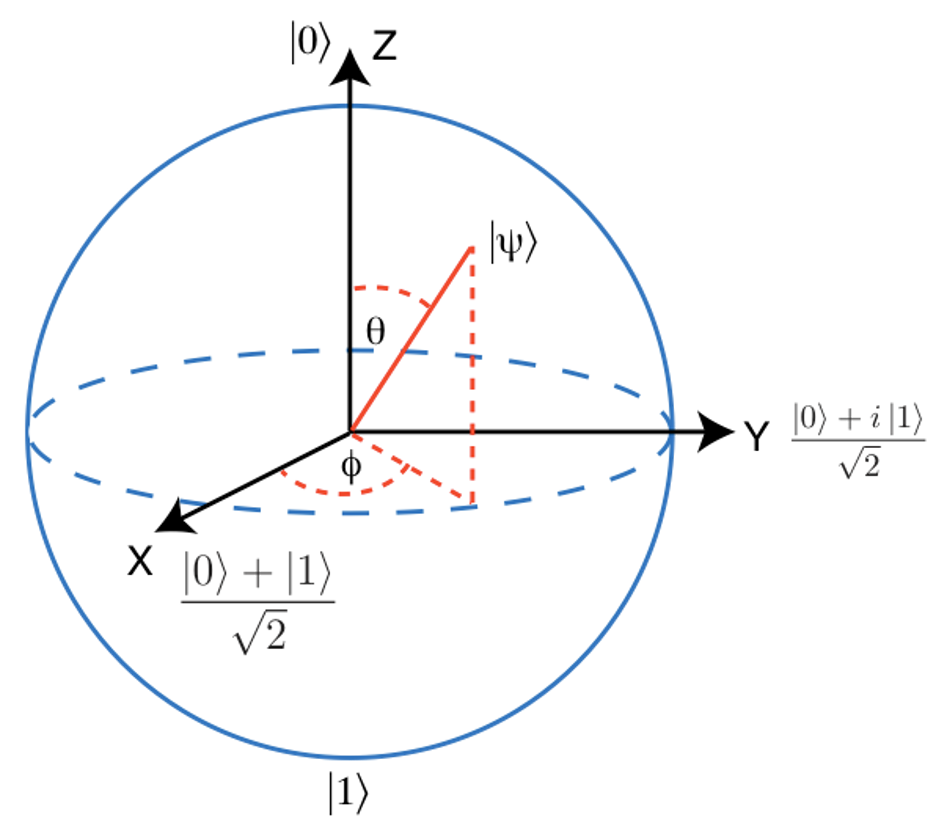
The electron spin can have any orientation, but any measurement of its x- or y- or z-component yields two separated beams unless the spins of all incoming beam electrons were oriented in one of the eigenstates of the corresponding component. The orientation of the electon spin can be illustrated by considering the electron spin as vector of unit length starting at the center of a sphere (so called Bloch sphere) and pointing to an arbitrary point on the sphere's surface. However, it only takes one of 2 possible states when measured. Compared to the bits of a digital (classical) system, which can only have exactly one of the 2 possible real values (0 or 1), a 2-state quantum system can take any point on the Bloch sphere.
|
Spins can point in any direction on the Bloch sphere. A point on the Bloch sphere is
described by two angles, θ (relative to the |0> direction) and φ (relative
to the |+x> direction): |ψ>=cos(θ/2) |0> + eiφ sin(θ/2) |1> Note that this is not a standard sphere in the 3-dimensional real space, but a sphere in a 2-dimensional complex space. Vectors, which point in opposite directions, are orthogonal to each other: their inner product, i.e. their projection onto each other, vanishes: <χ|ψ>=0, for instance: <0|1>=0 |
Access tokens to IonQ's systems can be provided to all UMD students, faculty, staff,
and affiliates. Please contact fklein@umd.edu
for assistance.
Back to Top